Beim Quiz im letzten QUA handelt es sich um eine alte Frage, die 1958 in einer Kolumne der Zeitschrift Scientific American vom Rätsel-Guru Martin Gardner gestellt worden ist und seither für viel beschriebenes Papier und Kopfweh bei Studenten gesorgt hat. Das Problem lässt sich mit der richtigen Idee sofort lösen und als nettes Problemchen beiseite legen. Im Hintergrund gibt es jedoch interessante Querverbindungen zu Mathematik/Statistik und Physik, die in diesem Artikel nur erwähnt werden können.
Wir lösen den Fall des Würfels, wenn an diagonal gegenüberliegenden Ecken eine Spannung angelegt (oder der Widerstand gemessen) wird. Die entscheidende Erkenntnis ist die, dass die 3 benachbarten Ecken aus Symmetriegründen auf dem gleichen elektrischen Potential liegen und deshalb zusammengelötet werden können. Man kann die Gitter auch flachgedrückt so zeichnen, dass die y-Koordinate das elektrische Potential angibt. Als Beispiel der Würfel mit 5 Volt:
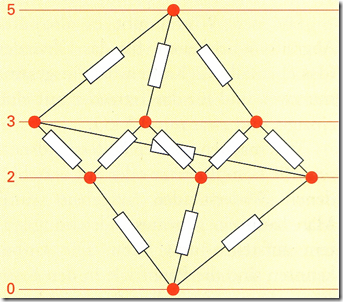
Man bekommt eine Reihenschaltung von 1/3 + 1/6 + 1/3 = 5/6 Ohm. Bei den zwei weiteren Abgreifmöglichkeiten (“nächste” Ecken d.h. direkt benachbart, oder auf einer Seitenfläche diagonal gegenüber) ergeben sich 7/12 Ohm und 3/4 Ohm. Das Dodekaeder und andere räumliche Widerstandsgitter lassen sich genau gleich lösen:
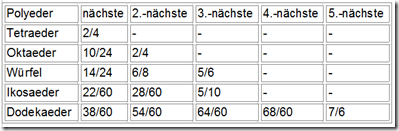
Als weiteres Beispiel der Dodekaeder mit der Spannung an diagonal gegenüberliegenden Ecken:
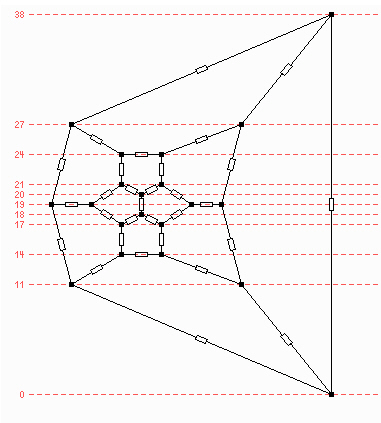
Der Widerstand ist 38/60. Die Brüche in der Tabelle sind so gewählt, dass alle Spannungen (hier 38V) und Ströme (hier 60A) auf allen Leitungen ganzzahlig sind.
In einem Artikel in Spektrum der Wissenschaft 2006/8 wurde eine alte Querverbindung zur Mathematik wieder aufgezeigt: man nehme ein Quadrat aus dünnem Blech, löte an an zwei gegenüberliegenden Kanten dicke (ideal leitende) Drähte an. Der Widerstand ist dann unabhängig von der Grösse des Quadrates, da er proportional zum Abstand und umgekehrt proportional zur Länge der Drähte (=Breite) ist! Der Widerstand sei 1 Ohm. Wir nehmen so ein Rechteck und legen oben und unten eine Spannung an. Dann ist das Potential proportional zur Höhe (y-Koordinate). Ohne dass sich daran etwas ändert, kann man vertikale Schlitze ins Blech schneiden oder horizontale Drahtstücke auflöten. Auch kann man rechteckige Stücke durch einen entsprechenden gewöhnlichen Widerstand ersetzen. So entspricht eine Zerlegung des Blechrechtecks einem Widerstandsnetzwerk aus gewöhnlichen Widerständen! Als Beispiel der Würfel (rot=Drähte, weiss=Schlitze im Blech):
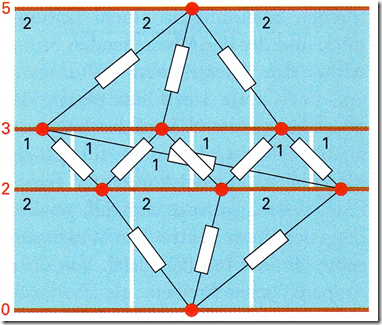
Über die Zerlegungsmöglichkeiten eines Rechtecks in kleinere Quadrate ist übrigens auch heute noch nicht alles bekannt!
Man wird sicher zustimmen, dass die Bestimmung des Widerstandes von solchen komplizierten räumlichen Widerstandsnetzwerken prinzipiell zwar mit den Kirchhoff’schen Regeln möglich ist, aber praktisch nur Cleverness oder ein Computer zum Ziel führt. Auch für Computerprogramme brauchts ziemlich viel Lineare Algebra und Numerik. Schwierig wird es spätestens bei Gebilden, die nicht mehr aus diskreten Widerständen aufgebaut sind, z.B. aus Blech. Solche Probleme sind nur mit höheren Methoden lösbar (harmonische Analyse, Potentialtheorie). Die üblichen Kirchhoff’schen Gesetze sind nur sehr einfache Spezialfälle davon.
Referenzen:
Spektrum der Wissenschaft, August 2006 (http://www.spektrum.de/artikel/848575).
F. Y. Wu, Theory of resistor networks: the two-point resistance, J. Phys. A: Math. Gen. 37 (2004) 6653–6673.
Neues Quiz
Frage 1) Der Lehrling von Elektriker R. Öhrli hat gebastelt – seine Schaltung besteht aus einer Batterie, drei gleichen Glühlampen, einem Umschalter (Wechselschalter) und Kabeln. Es brennen alle Lampen. Der Schalter wird umgeschaltet. Wieder leuchten alle Lampen, diesmal alle mit einer anderen Leuchtstärke als vorher. Wie sieht die Schaltung aus?
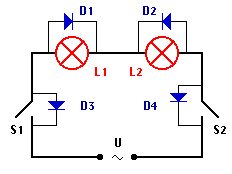 Frage 2) An dieser Schaltung liegt eine Wechselspannung:
Frage 2) An dieser Schaltung liegt eine Wechselspannung:
Welche Lampe/n leuchtet/leuchten, wenn nur Schalter S1 geschlossen wird? Und wenn nur S2 geschlossen wird? Und wenn beide zu sind?